권오흠 교수님의 '영리한 프로그래밍을 위한 알고리즘' 강의를 학습한 기록입니다.
Recursion vs. Iteration
- 모든 순환함수(Recursion)는 반복문(Iteration)으로 변경이 가능하다. 그 역도 성립한다.
- 순환함수 장단점
- 장점 : 복잡한 알고리즘을 단순하고 알기 쉽게 표현 가능
- 단점 : 오버헤드 발생 (매개변수 전달, 액티베이션 프레임 생성 등)
Recursion 설계
원칙
• 적어도 하나 이상의 순환이 종료되는 base case가 있어야 한다.
• 모든 case는 결국 base case로 수렴해야 한다.
방법
암시적(implicit) 매개변수를 명시적(explicit) 매개변수로 바꿔라.
예시를 통해 알아보자.
⚡︎ 순차 탐색(Sequential Search)
‣ 순차 탐색은 처음부터 끝까지 하나씩 찾아보는 방법이다.
int search(int[] data, int n, int target){
for(int i=0; i<n; i++) {
if(data[i] == target)
return i;
}
return -1;
}이 함수의 목적은 data[0]에서 data[n-1] 사이의 target을 검색하는 것이다. 여기서 보통 검색 구간의 시작 인덱스인 0은 생략한다. 즉, 암시적 매개변수이다.
이를 순환함수로 바꿔보자.
int search(int[] data, int begin, int end, int target){
if(begin > end)
return -1;
else if(target == data[begin])
return begin;
else
return search(data, begin+1, end, target);
}함수의 시작지점을 data[begin]으로 명시화 하였다. 앞서 반복문 함수에서 "배열 전체를 순환하겠다" 와 달리 "begin 확인 후, 동일한 함수로 다음 확인해야할 값들을 지정"하는 방법을 결정하는 것이 중요하다. 여기서는 begin+1 로 표현되어 있다. 여기서 base case는 확인해야할 남은 데이터가 0개가 되는 경우이다.
✔︎ 참고
위 순차탐색의 다른 버전이 있다. 참고로 확인해보자.
1) 끝부터 탐색
int search(int[] data, int begin, int end, int target){
if(begin > end)
return -1;
else if(target == data[end]) // 수정 1
return end;
else
return search(data, begin, end-1, target); // 수정 2
}
2) 반으로 나눠 한 쪽씩 탐색
int search(int[] data, int begin, int end, int target){
if(begin > end)
return -1;
else {
int middle = (begin + end)/2;
if(data[middle] == target)
return middle;
int index = search(data, begin, middle-1, target);
if(index != -1)
return index;
else
return search(data, middle+1, end, target);
}
}위 방법은 binary search와는 다르다.
⚡︎ 최대값 찾기
int findMax(int[] data, int begin, int end){
if(begin == end)
return data[begin];
else
return Math.max(data[begin], findMax(data, begin+1, end));
}순차탐색 예시와 마찬가지로 begin확인 후, begin+1으로 표현하여 다음 확인할 값들을 지정하였다. base case도 마찬가지라 확인해야할 남은 데이터가 0이 되는 경우이다.
⚡︎ 이진 탐색(Binary Search)
public static int binarySearch(String[] items, String target, int begin, int end){
if(begin > end)
return -1;
else{
int middle = (begin + end)/2;
int compResult = target.compareTo(items[middle]);
if(compResult == 0)
return middle;
else if(compResult<0)
return binarySearch(items, target, begin, middle-1);
else
return binarySearch(items, target, middle+1, end);
}
}이진 탐색은 자료가 순서대로 정렬되어있음을 전제로 한다. 이진 탐색은 근본적으로 순환의 구조로 동작한다.
Recursion 응용
미로 찾기(Maze)
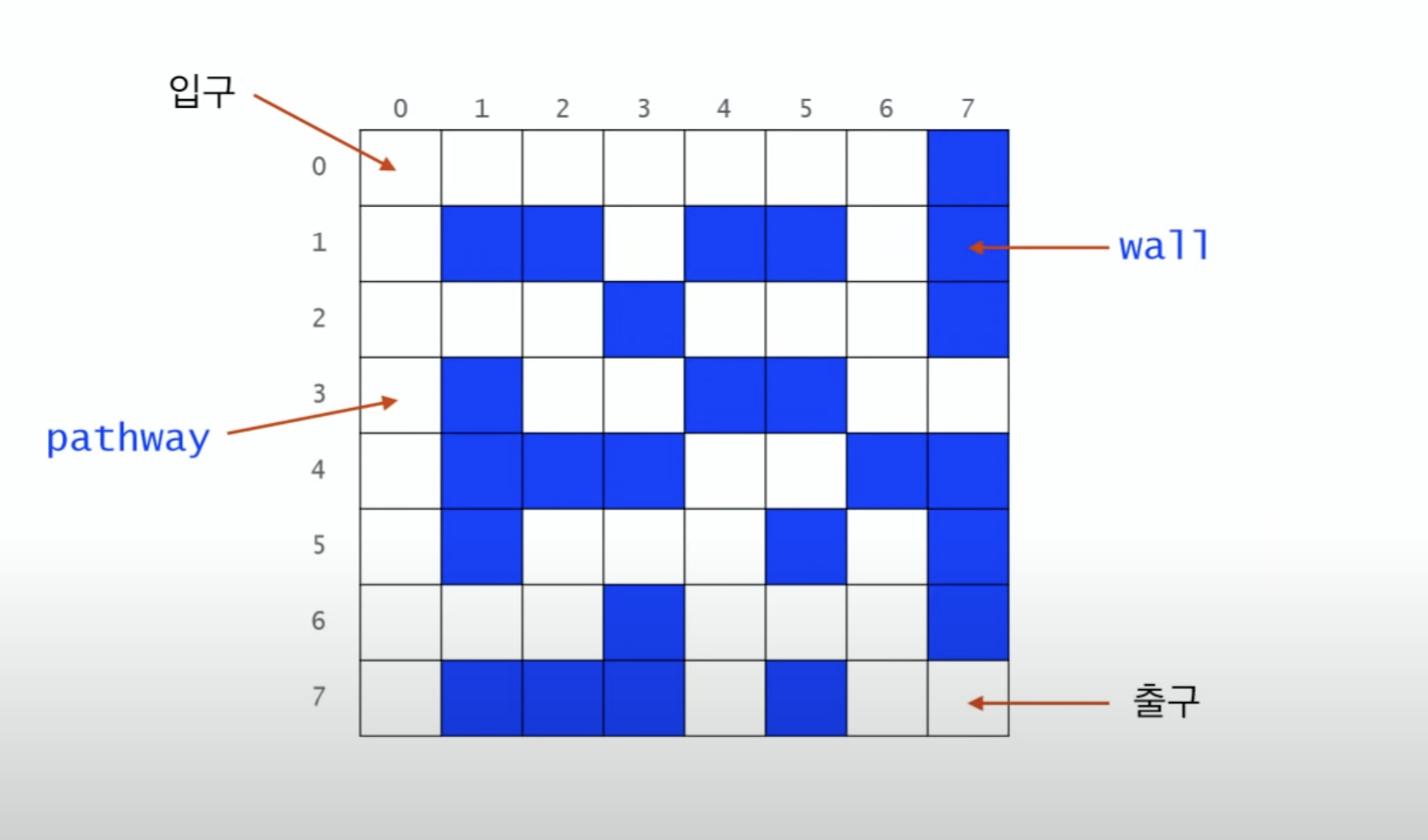
흰색 칸이 길이고 파란색 칸이 벽이다. 위 그림에서는 8*8로 표현되어 있지만, N*N으로 일반화할 수 있다.
Recursive 하게 설계해보자.
• 현재 위치가 출구이거나
• 이웃한 칸 중에서 현재 위치를 다시 지나지 않고 출구까지 가는 경우가 있거나
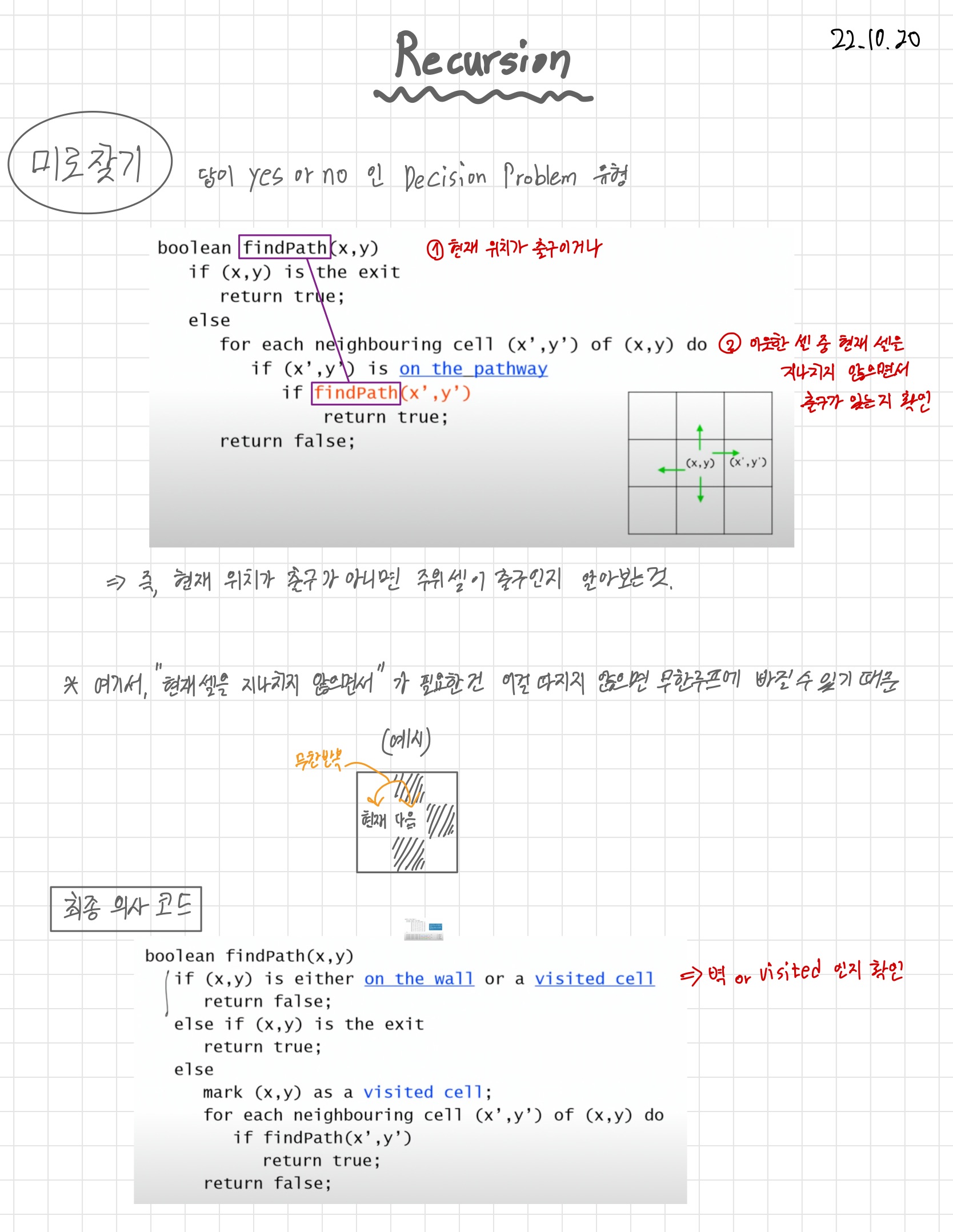
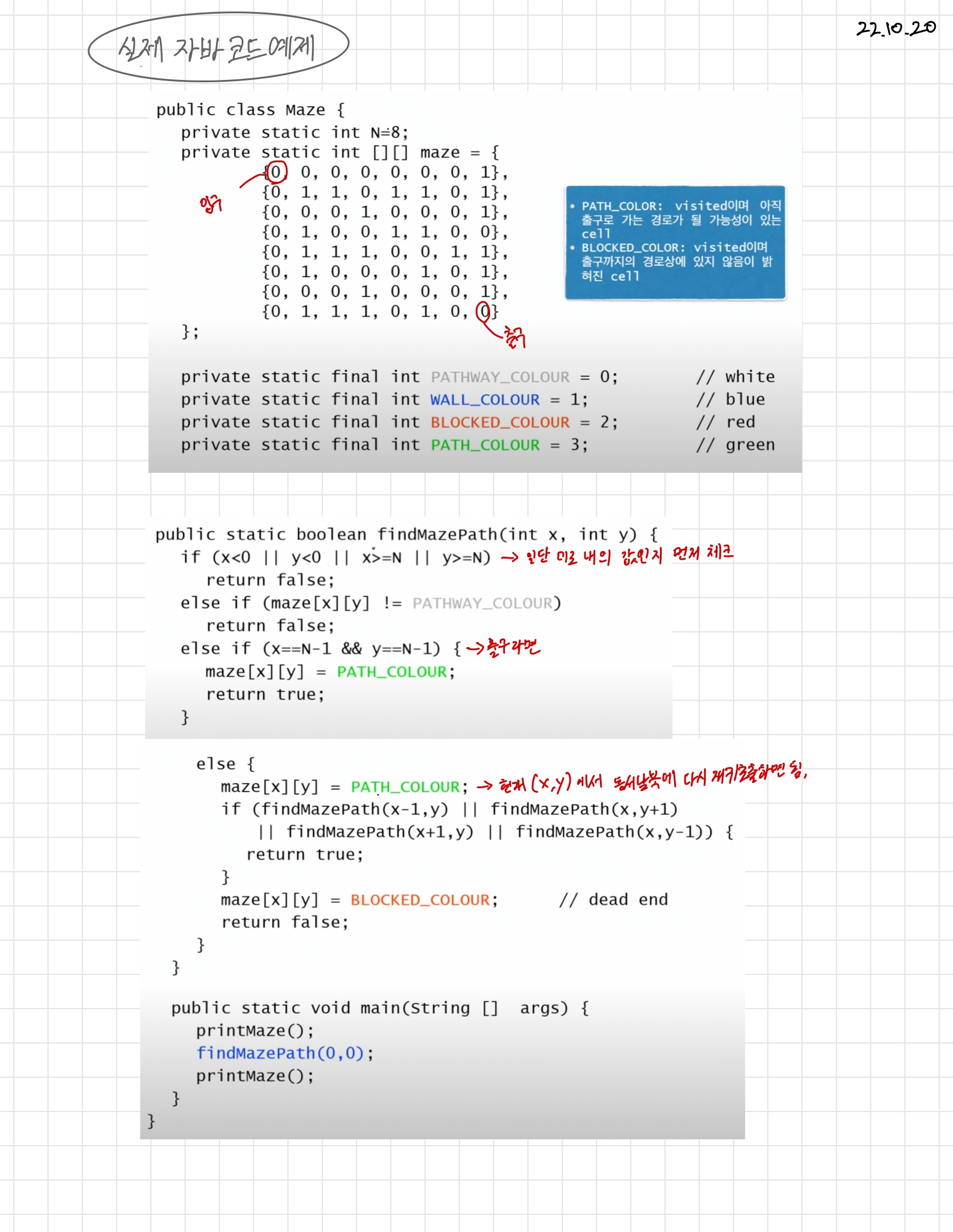
'알고리즘 > 이론' 카테고리의 다른 글
| 합병정렬 merge sort (0) | 2022.10.26 |
|---|---|
| [기본적인 정렬 : selection, bubble, insertion sort] (0) | 2022.10.25 |
| Recursion #4 [멱집합, power set] (0) | 2022.10.22 |
| Recursion #3 [N queens problem] (0) | 2022.10.21 |
| Recursion #2 [counting cells in a blob] (0) | 2022.10.21 |
